3 Variables Aleatorias
3.1 Distribuciones incorporadas en R
Puede encontrar una lista de las distribuciones de probabilidad disponibles en el paquete stats (incorporado en R) ejecutando ?Distributions.
?Distributions| Función | Función de R |
|---|---|
| Función distribución acumulada (CFD) | pxxx |
| Función quantil (inversa de la CFD) | qxxx |
| Funcion densidad o masa de probabilidad | dxxx |
| Generación de variables aleatorias | rxxx |
3.1.1 Distribución Normal
3.1.1.1 Funcion distribución acumulada pnorm
Example 3.1 Supon que el peso de una probeta de concreto está normalmente distribuido con media 12.7kg y desviación estandar 0.45kg. ¿Cuál es la probabilidad de que una probeta escogida aleatoriamente pese más de 13kg?
Parafraseo Si \(X\) tiene distribución \(\mathcal{N}(12.7,0.45^2)\), hallar \(P(X > 13)\).
Usando pnorm
1 - pnorm(13, mean = 12.7, sd = 0.45)## [1] 0.2524925:::
3.1.1.2 Función quantil qnorm
Example 3.2 Supon que las pruebas de IQ están normalmente distribuidas con media 100 y desviación estandar 15. ¿Cuál es el 95 percentil de la distribución de IQ?
Parafraseo Si \(X\) tiene distribución \(\mathcal{N}(100, 15^2)\), hallar \(F^{-1}(0.95)\).
Usando pnorm
qnorm(0.95, mean = 100, sd = 15)## [1] 124.6728
3.1.1.3 Función densidad dnorm
En el caso continuo, no hay mucha necesidad de esta función, ya que para calcular probabilidades se usa pnorm.
Sin embargo podemos graficarlo.
curve(dnorm, from = -3, to = 3)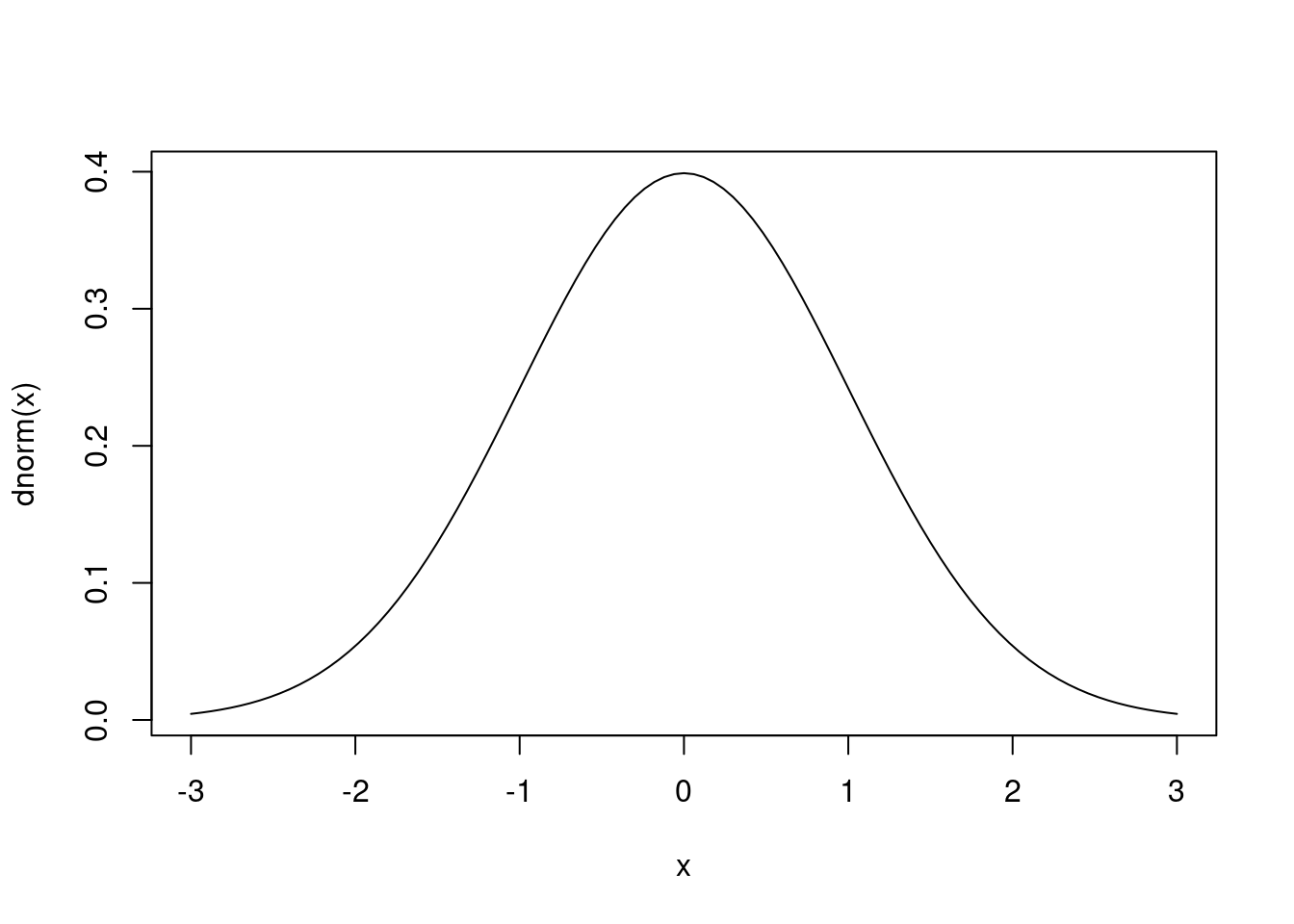

3.1.1.4 Generación de variables aleatorias rnorm
En el caso continuo, no hay mucha necesidad de esta función, ya que para calcular probabilidades se usa pnorm.
Sin embargo podemos graficarlo.
set.seed(42)
x <- rnorm(10000, mean = 12.7, sd = 0.45)
hist(x, probability = T)
curve(dnorm(x, 12.7, 0.45), from = 11, to = 14.5, add = T)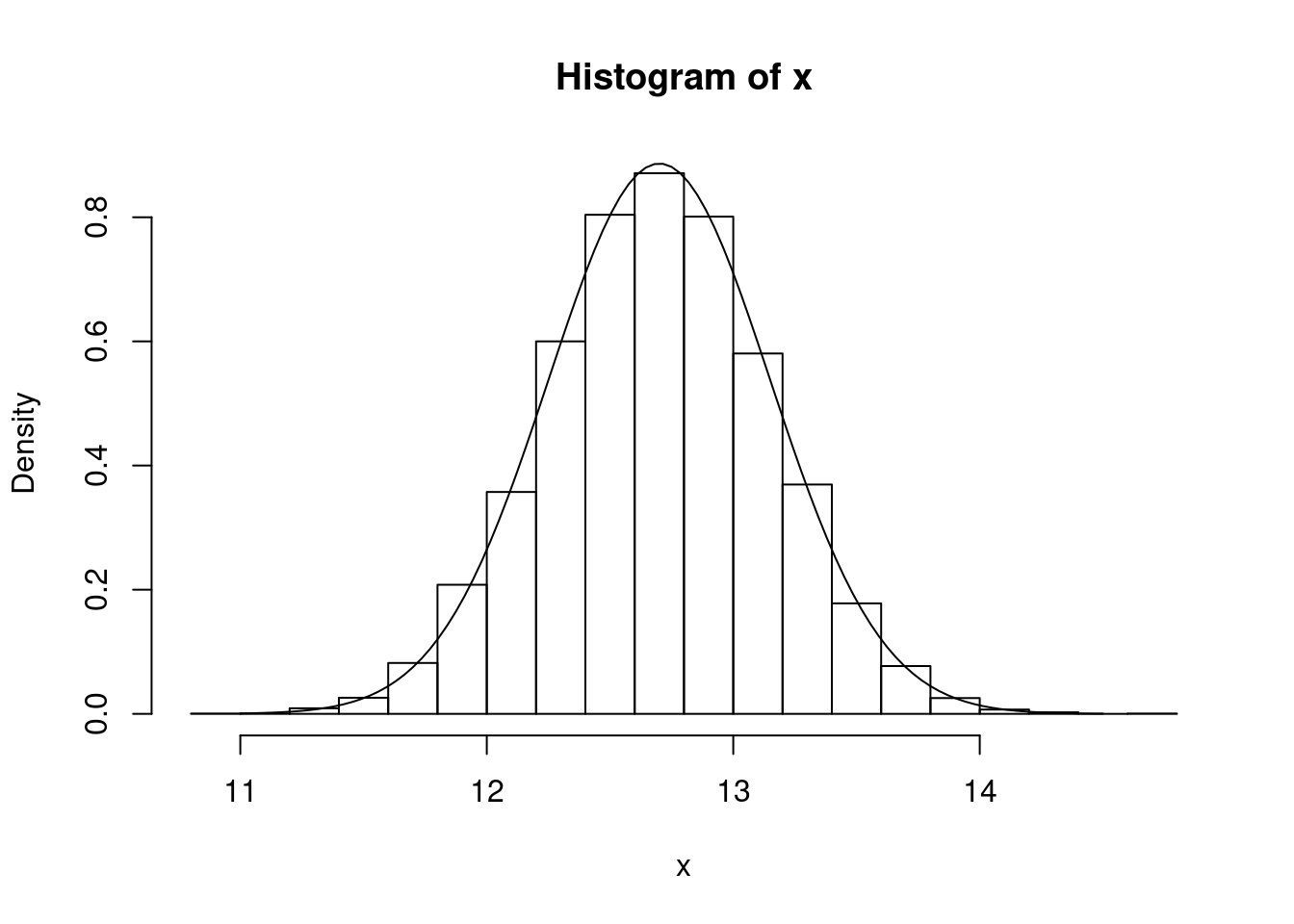
3.1.2 Distribución Binomial
3.1.2.1 Función densidad dbinom
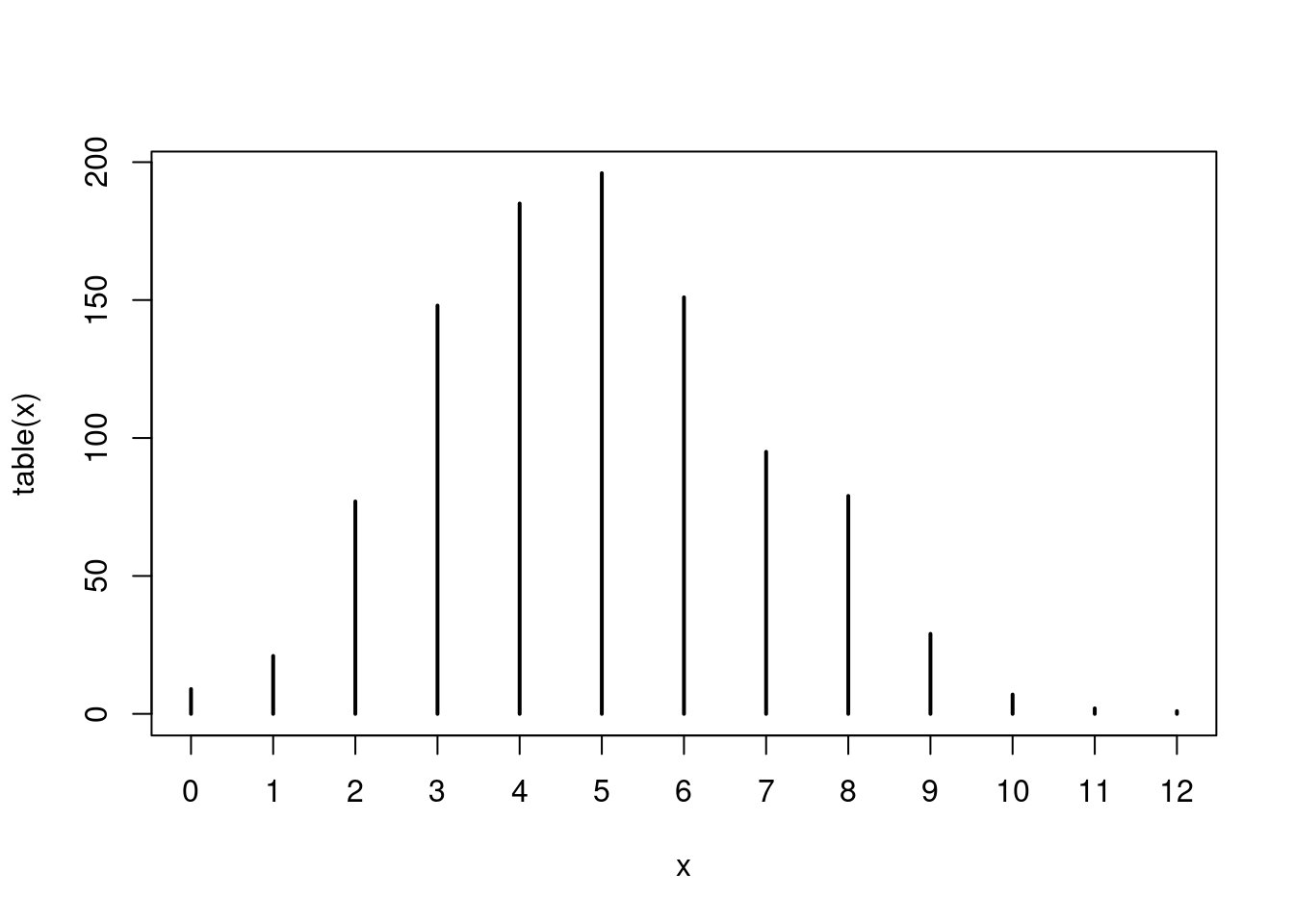
Example 3.3 Supon que un foco tiene una probabilidad de 0.2 de tener defectos. Supon que un contenedor contiene 25 focos ¿Cuál es la probabilidad de que un contenedor escogido aleatoriamente tenga exactamente 1 foco defectuoso?
Parafraseo Si \(X\) tiene distribución \(\mathcal{Bin}(25, 0.2)\), hallar \(P(X=1)\).
Usando dbinom
dbinom(1, size = 25, prob = 0.2)## [1] 0.02361183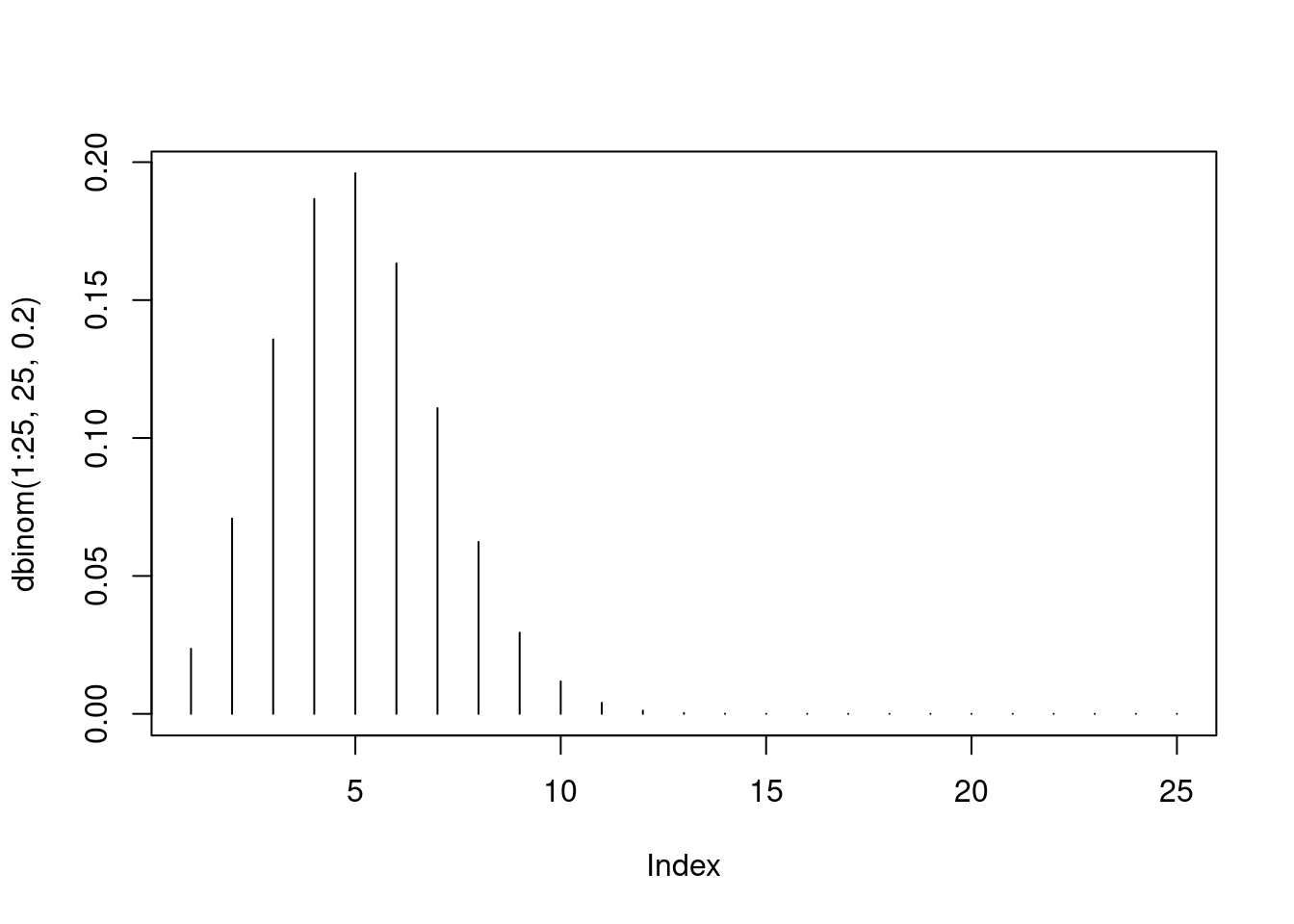
3.1.2.2 Función distrubción acumulada pbinom
Example 3.4 Supon que un foco tiene una probabilidad de 0.2 de tener defectos. Supon que un contenedor contiene 25 focos. ¿Cuál es la probabilidad de que un contenedor escogido aleatoriamente tenga a lo más un foco defectuoso?
Parafraseo Si \(X\) tiene distribución \(\mathcal{Bin}(25, 0.2)\), hallar \(P(X \le 1)\).
Usando pbinom
pbinom(1, size = 25, prob = 0.2)## [1] 0.02738973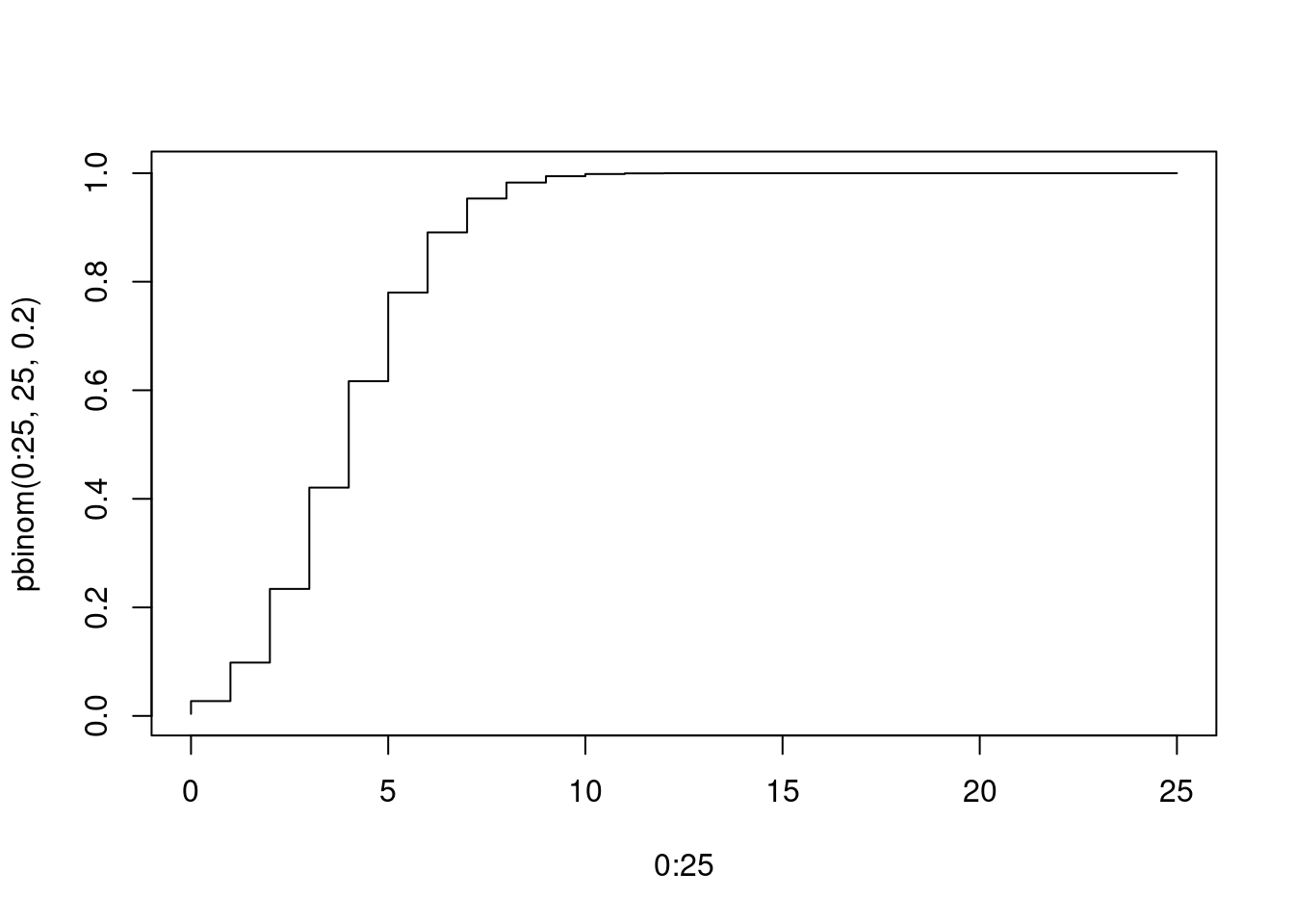
rval <- approxfun(
0:25, pbinom(0:25, 25, 0.2),
yleft = 0, yright = 1, ties = "ordered", method = "constant"
)
class(rval) <- c("ecdf", "stepfun", class(rval))
plot(rval, main = "Distribución Binomial", ylab = "Probabilidad")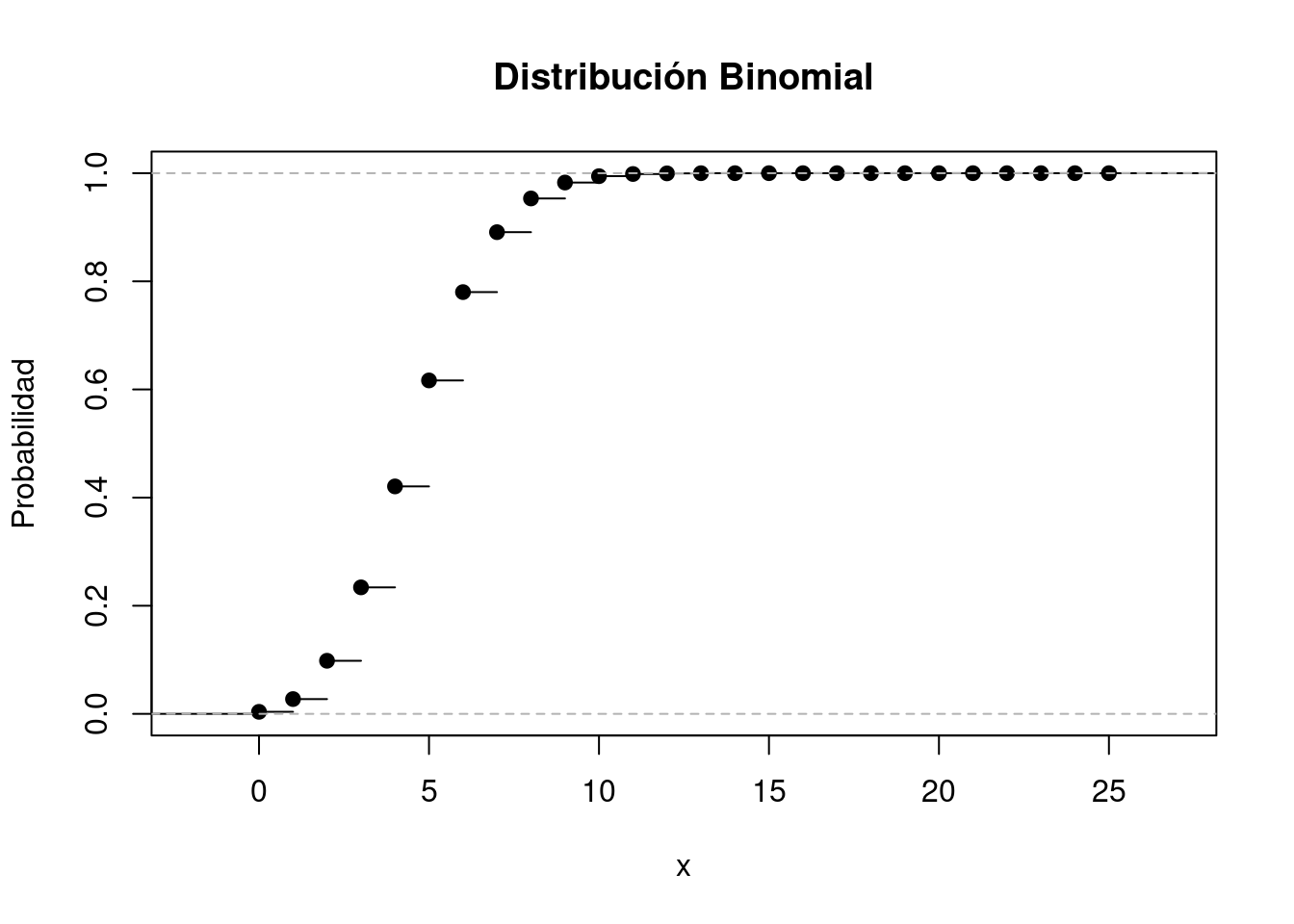
3.2 Generación de números aleatorios de otras distribuciones
3.2.1 Transformación inversa
Fuente: Christian Robert, George Casella - Montecarlo Statistical Methods - Springer
Definition 3.1 (Inversa generalizada) Para una función distribución \(F\) en \(\mathbb{R}\), la inversa generalizada de \(F\), \(F^-\), está definida por \[ F^{-}(u) = \inf\{x : F(x) \ge u\}. \]
El siguiente lema nos da una representación de cualquier variable como una transformación de una variable aleatoria uniforme.
Lemma 3.1 Si \(U \sim \mathcal{U}_ {[0, 1]}\), entonces la variable aleatoria \(F^-(U)\) tiene distribución \(F\).
Proof. Para todo \(u \in [0, 1]\) y para todo \(x \in F^-([0, 1])\), la función inversa generalizada satisface \[ F(F^-(u)) \ge u \text{ y } F^{-}(F(x)) \le x. \] Entonces, \[ \{(u, x) : F^{-}(u) \le x \} = \{(u,x) : F(x) \ge u\} \] y \[ P(F^-(U) \le x) = P(U \ge F(x)) = F(x) \]
Example 3.6 (Distribución Exponencial) Si \(X \sim \mathcal{Exp}(1)\), así \(F(x) = 1-e^{-x}\), luego \(F^-(u) = -\log(1 - u)\). Entonces, por el lema 3.1 \(X = F^-(U) = -\log(1 - U) = -\log(U)\).
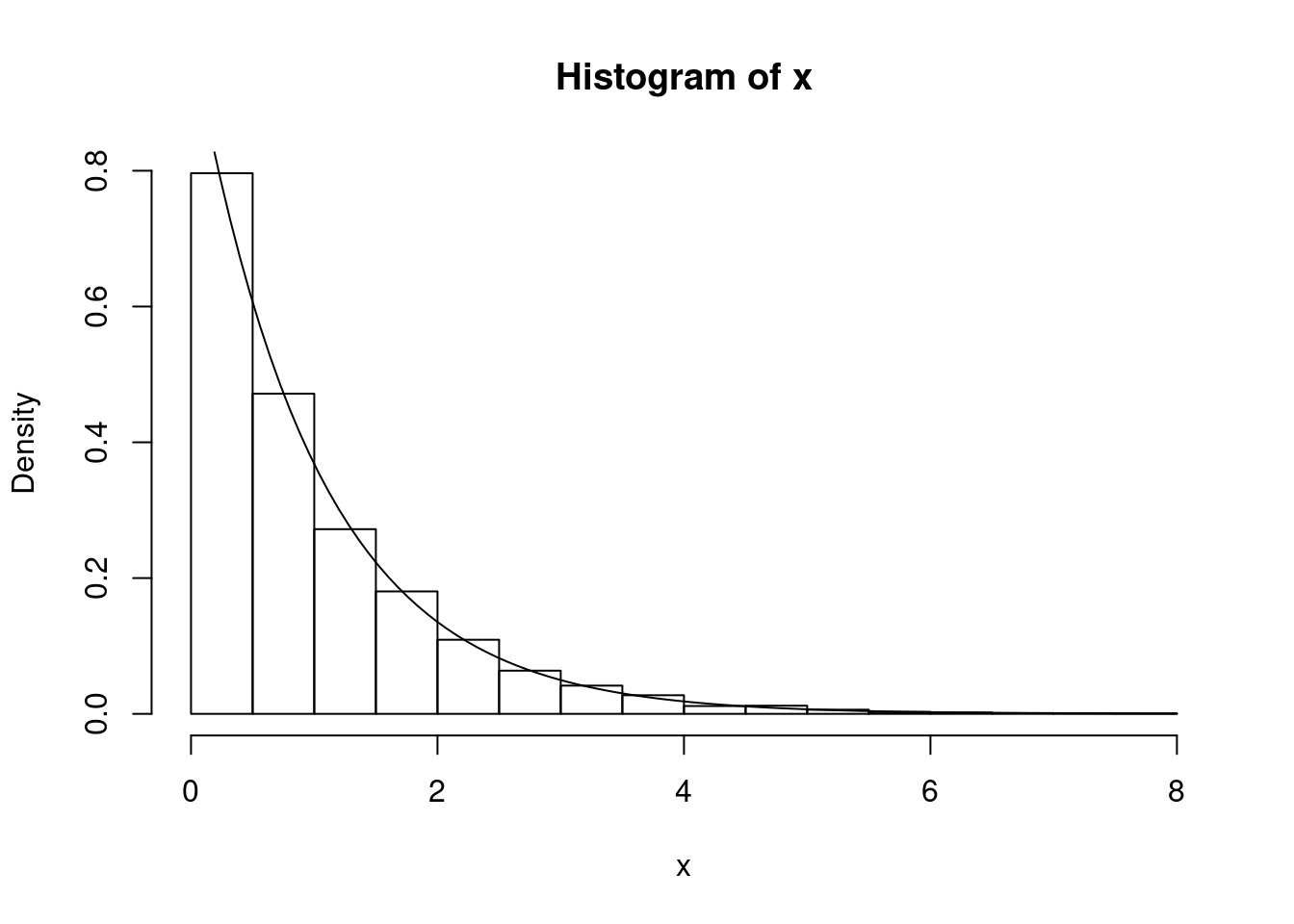
Example 3.7 (Distribución Triangular) Generamos una muestra aleatoria de una distribución triangular de mínimo \(a\), moda \(b\) y máximo \(c\). \[ f = \begin{cases} \frac{2(x-a)}{(c-a)(b-a)} & x \in [a,b] \\ \frac{2(x-c)}{(c-a)(b-c)} & x \in [b,c] \end{cases} \]
f <- function(x, a, b, c) {
ifelse(
x < b,
2 * (x - a) / ((c - a) * (b - a)),
2 * (x - c) / ((c - a) * (b - c))
)
}
a <- 1
b <- 2
c <- 3
curve(f(x, a, b, c), from = a, to = c)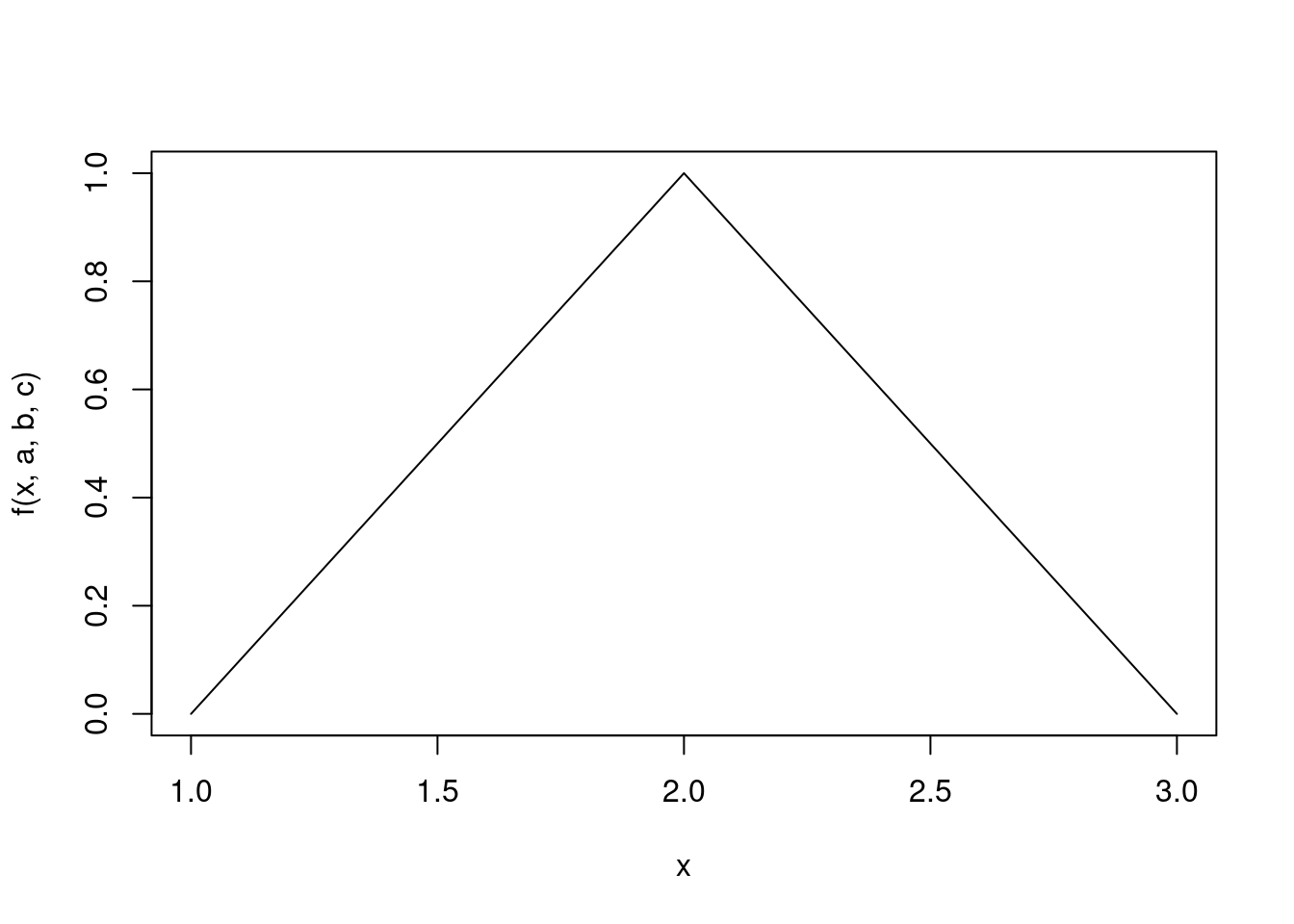
\[ F^-(p) = \begin{cases} \sqrt{(c-a)(b-a)p} + a & p \in \left[0, \frac{b-a}{c-a}\right] \\ -\sqrt{(c-a)(b-c)(p-1)} + c & p \in \left[\frac{b-a}{c-a}, 1\right] \end{cases} \]
set.seed(42)
F_inv <- function(p, a, b, c) {
ifelse(
p < (b - a) / (c - a),
sqrt((c - a) * (b - a) * p) + a,
-sqrt((c - a) * (b - c) * (p - 1)) + c
)
}
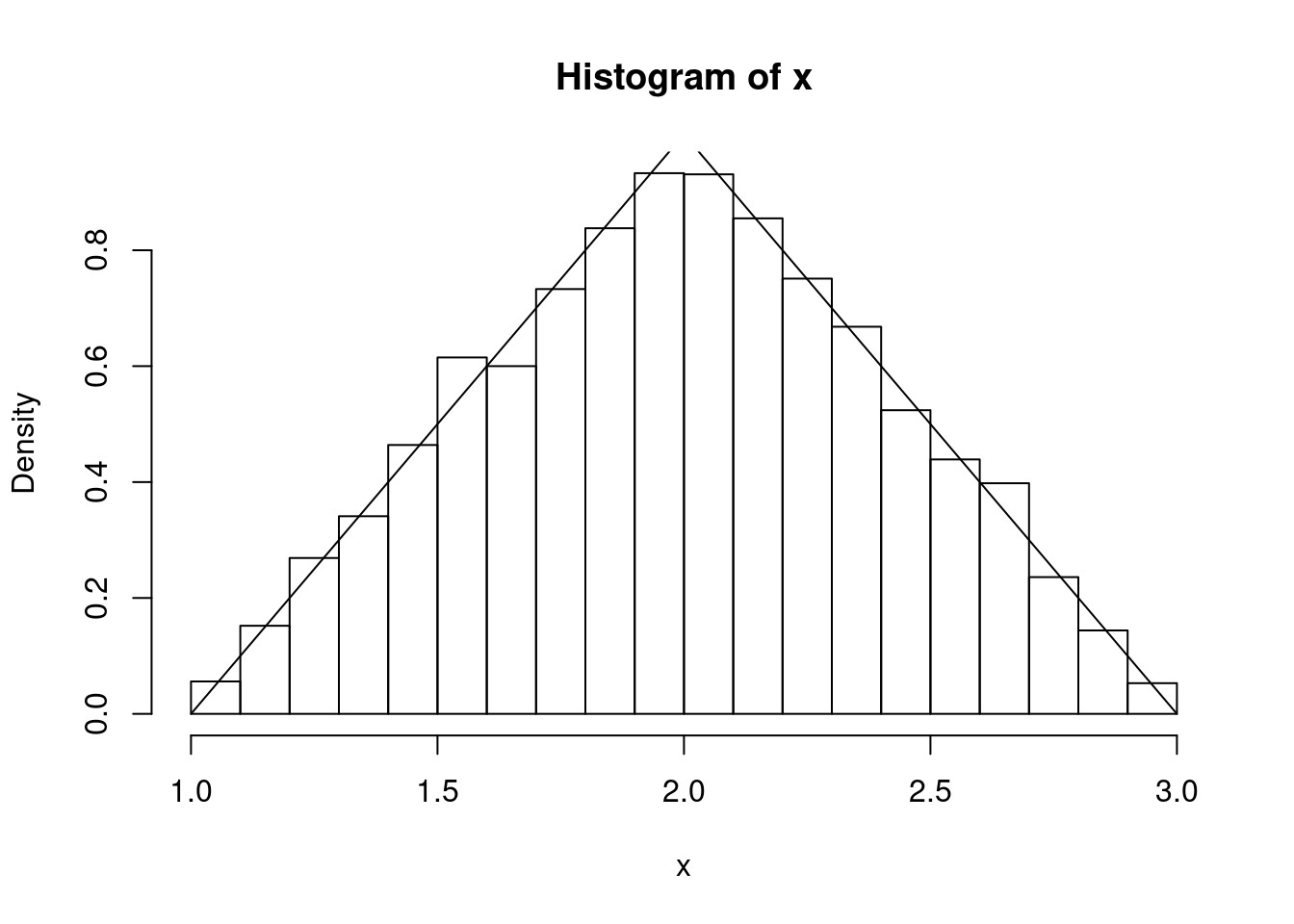
x <- F_inv(runif(10000), a = 1, b = 2, c = 3)
hist(x, probability = T)
curve(f(x, a, b, c), from = a, to = c, add = T)