1 Conteo y Probabilidad

1.1 Problema de cumpleaños

Hay \(k\) personas en un cuarto. Supon que los cumpleaños de cada persona son igualmente probables de ocurrir en los \(365\) días del año, y los cumpleaños son independientes. Cuál es la probabilidad que al menos haya un par de personas con el mismo cumpleaños.

1.1.1 Usando un contador

set.seed(42)
n <- 100  # número de simulaciones
k <- 10  # número de personas
count <- 0
for (i in 1:n) {
  x <- sample(365, k, replace = T)
  coinciden <- any(table(x) > 1)
  if (coinciden) {
    count <- count + 1
  }
}
count / n

## [1] 0.13

1.1.2 Usando vectores

set.seed(42)
n <- 100  # número de simulaciones
k <- 10  # número de personas
y <- rep(0, n)
for (i in 1:n) {
  x <- sample(365, 10, replace = T)
  y[i] <- any(table(x) > 1)
}
mean(y)

## [1] 0.13

1.1.3 Usando `replicate`

set.seed(42)
n <- 100  # número de simulaciones
k <- 10  # número de personas
x <- replicate(n, any(table(sample(365, k, replace = T)) > 1))
mean(x)

## [1] 0.13

1.2 Matching problem de De Montmort

Considera un mazo de \(n\) cartas bien barajadas y etiquetadas del \(1\) al \(n\). Vas volteando las cartas uno a uno, diciendo los numeros del \(1\) al \(n\). Ganas el juego si, en algún punto, el número dicho es el mismo de la etiqueta de la carta volteada. ¿Cuál es la probabilidad de ganar?

set.seed(42)
n <- 10  # número de cartas
y <- replicate(1000, any(sample(n) == 1:n))
mean(y)

## [1] 0.658

1.3 Error de Leibniz

Si se lanzan dos dados, ¿es más probable que la suma sea 11 o que sea 12?

set.seed(42)
n <- 2000
dado1 <- sample(6, n, replace = T)
dado2 <- sample(6, n, replace = T)

La probabilidad de que la suma sea 11

mean(dado1 + dado2 == 11)

## [1] 0.0565

La probabilidad de que la suma sea 12

mean(dado1 + dado2 == 12)

## [1] 0.0275

1.4 Full house en poker

¿Cuál es la probabilidad de un full house?

set.seed(42)
x <- replicate(20000, {
  mano <- sample(52, 5)
  table_mano <- table(mano %% 13)
  all(2 <= table_mano & table_mano <= 3)
})
mean(x)

## [1] 0.0013

1.5 Lema de Borel-Cantelli

Lemma 1.1 (Teorema de Borel-Cantelli) Si \(\displaystyle\sum_{n=1}^\infty {\mathrm{P}(A_n)} = \infty\) y los eventos \((A_n)_ {n=1}^\infty\) son independientes, entonces \(\displaystyle\mathrm{P}(A_n\text{ rec.}) = 1\)

Example 1.1 Sean \(q \in \mathbb{N}\), \(\Omega = \{0, 1\}^\mathbb{N}\) y \(A_n = \{\omega \in \Omega \,|\, \omega_{nq+1} = \omega_{nq+2} = \cdots = \omega_{(n+1)q-1} = 1\}\). Luego, por el lema 1.1, \(\displaystyle\mathrm{P}(A_n\text{ rec.}) = 1\).

Digamos que \(q = 4\). En una muestra \(\omega\), se cumplir que \(A_n\) sea recurrente. Primero encontramos los primeros 5 \(n\)’s que cumplen \(\omega \in A_n\)

set.seed(42)
q <- 4
monedas_lanzadas <- c()
exito <- c()
for (i in 1:5) {
  repeat {
    q_monedas_lanzadas <- sample(c(0, 1), q, replace = T)
    monedas_lanzadas <- c(monedas_lanzadas, q_monedas_lanzadas)
    if (all(q_monedas_lanzadas == 1)) {
      exito <- c(exito, T)
      break
    }
    exito <- c(exito, F)
  }
}
which(exito)

## [1]  2  5 12 14 19

Esos son los primeros 5 \(n\)’s que cumplen \(\omega \in A_n\). Ahora ploteamos la muestra. De rojo se muestra las veces que cumple.

color <- rep(ifelse(exito, "red", "black"), each = q)
cex <- rep(ifelse(exito, 1, 1), each = q)
plot(monedas_lanzadas, pch = 1, col = color, cex = cex)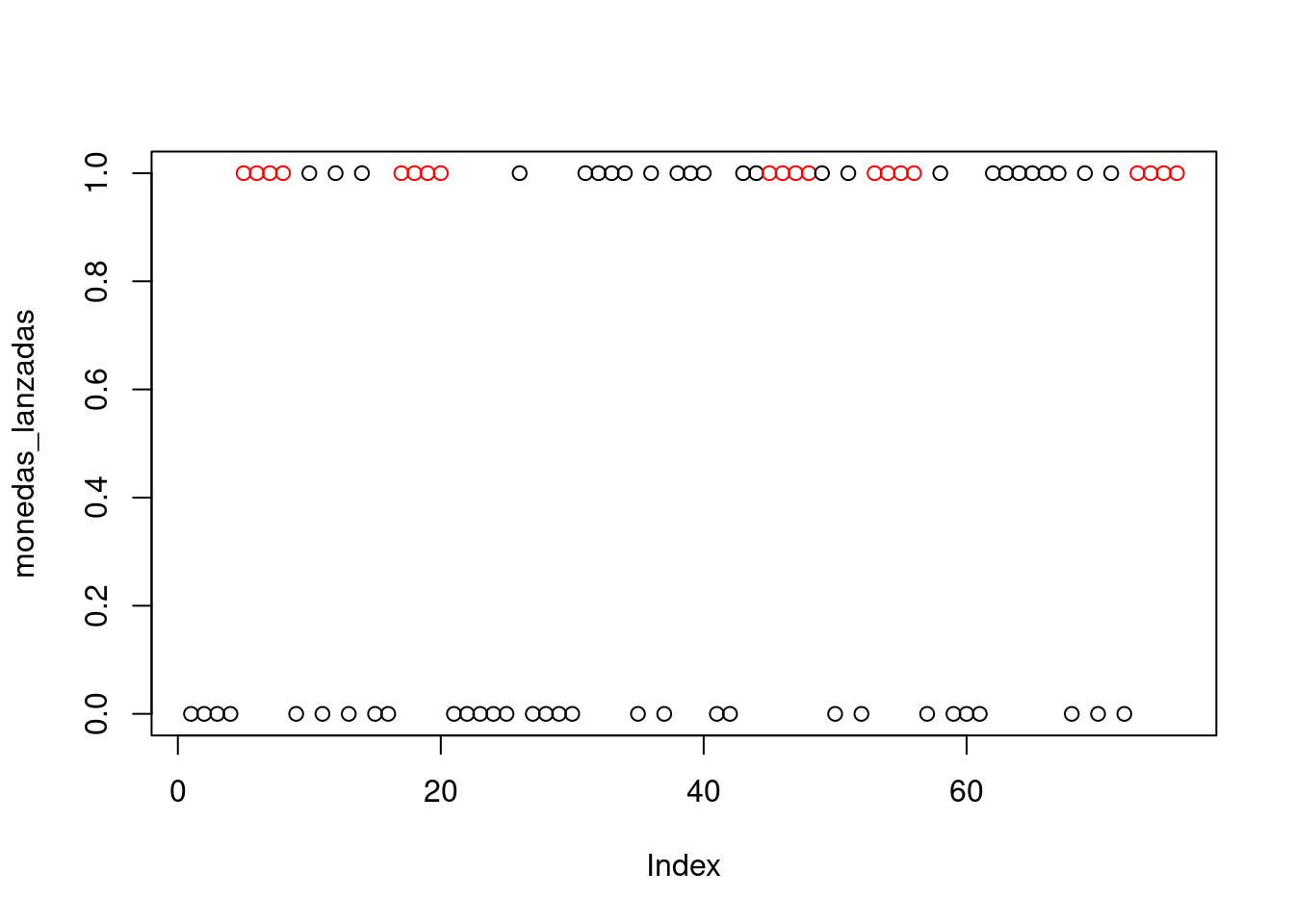

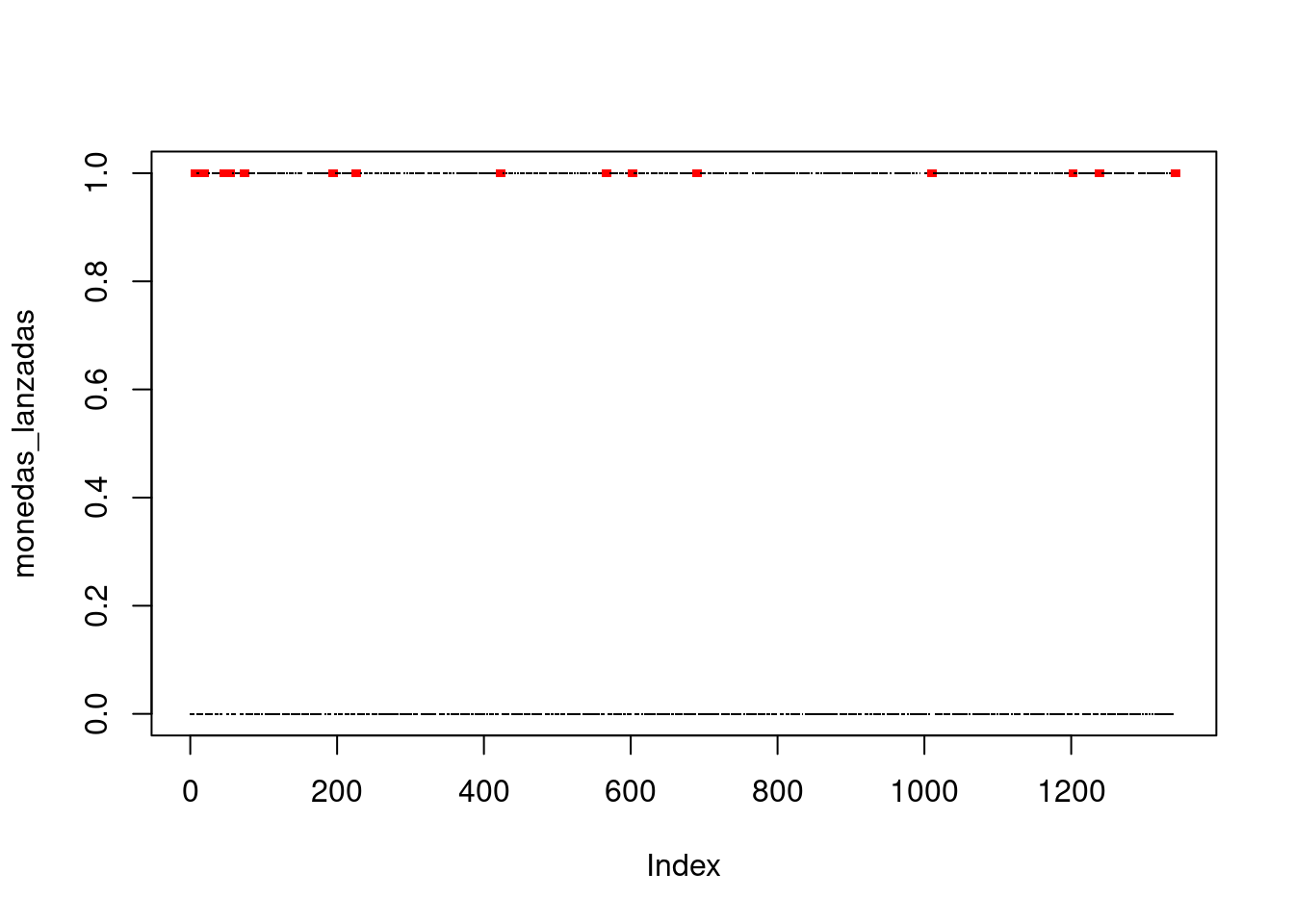
Ahora encontremos los 10 siguentes \(n\)’s que cumplen.

for (i in 1:10) {
  repeat {
    q_monedas_lanzadas <- sample(c(0, 1), q, replace = T)
    monedas_lanzadas <- c(monedas_lanzadas, q_monedas_lanzadas)
    if (all(q_monedas_lanzadas == 1)) {
      exito <- c(exito, T)
      break
    }
    exito <- c(exito, F)
  }
}
which(exito)

##  [1]   2   5  12  14  19  49  57 106 142 151 173 253 301 310 336

color <- rep(ifelse(exito, "red", "black"), each = q)
cex <- rep(ifelse(exito, 4, 1), each = q)
plot(monedas_lanzadas, pch = ".", col = color, cex = cex)

Prefacio

2 Probabilidad Condicional